Why We Use (n-1) For Sample Variance

That’s a fantastic question, and you are really curious about Machine Learning & AI — and it’s also the key to understanding statistics deeply! Let’s break it down in super easy words:

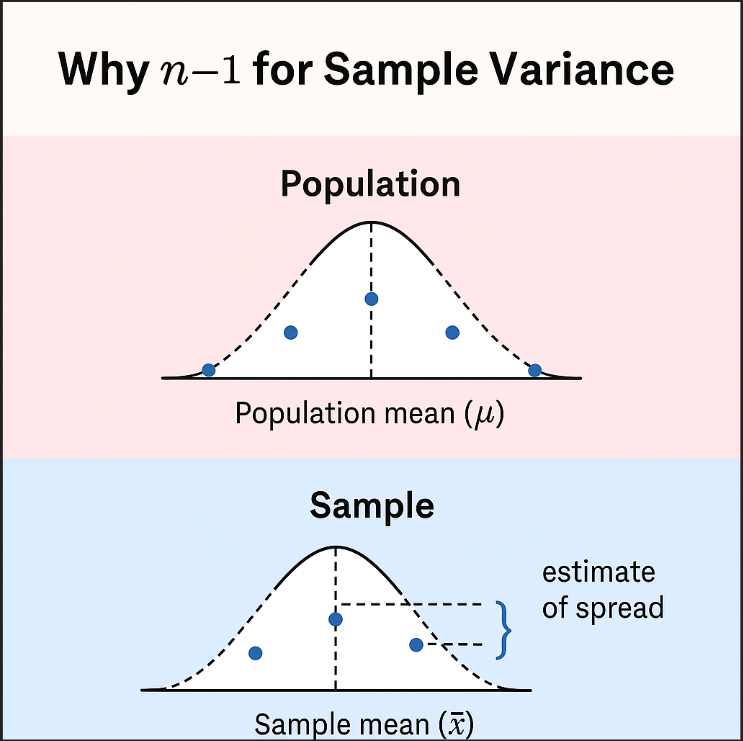
🔍 You’re trying to measure how spread out your data is (variance).

When you have the entire population, you just use the exact average (mean) and divide by how many items you have (n).

But…

🤔 When you’re only using a sample (a small piece of the full data):

You’re estimating the spread, not measuring the true one.

🧠 Here’s the logic:

When you calculate the mean from a sample, it is already pulled closer to the center than the actual population mean.

That makes the spread look a little smaller than it really is — it’s biased and underestimates the true variance.

🛠️ So what do we do?

We correct that bias by dividing by (n – 1) instead of n.

This is called Bessel’s correction, and it helps make the variance more accurate for samples.

🎨 Imagine this analogy:

You’re trying to guess how big a forest is, but you’re only allowed to look at 5 trees.
If you calculate the average tree height from just those 5, your guess is likely a little too close to the middle.
To make up for that, we slightly inflate the spread by dividing by one less tree → n - 1.

🔢 Simple Example:

data = [2, 4, 6]  # Sample of a bigger group

mean = 4
Sum of squared differences = (2-4)² + (4-4)² + (6-4)² = 4 + 0 + 4 = 8
Sample variance = 8 / (3 - 1) = 8 / 2 = 4

If we wrongly divided by 3 → we'd get 2.67 (too small!)

✅ Bottom line:

We subtract 1 (use n - 1) in sample variance to make sure our estimate isn’t too small and better reflects the true variance of the full population.